
Acest material despre operații cu numere reale cuprinde următoarele noțiuni: modulul unui număr real, adunarea și scăderea numerelor reale, înmulțirea și împărțirea numerelor reale, puterea unui număr real cu exponent întreg, raționalizarea numitorilor de forma a![]() , media aritmetică a n numere reale, media aritmetică ponderată a n numere reale, media geometrică a două numere reale și ecuația de forma
, media aritmetică a n numere reale, media aritmetică ponderată a n numere reale, media geometrică a două numere reale și ecuația de forma ![]() =a.
=a.
Modulul unui număr real:
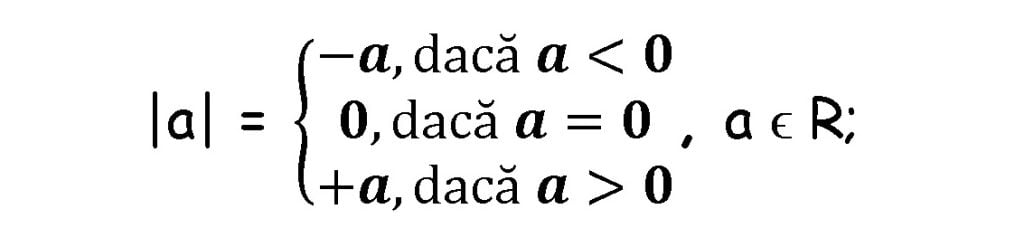
Exemple:
|-![]() | = – (-
| = – (-![]() ) =
) = ![]()
|+![]() | = +
| = +![]()
|![]() | = |
| = |![]() | = -(
| = -(![]() ) = –
) = –![]() = –
= –![]()
Adunarea și scăderea numerelor reale
Dacă a,b ϵ R atunci a+b ϵ R și a-b ϵ R.
Dacă termenii cuprind același radical, se scad/adună numerele din fața radicalului:
![]() ±
± ![]() = (a ± b)
= (a ± b)![]()
Exemplu: ![]() =
= ![]() =
= ![]()
Dacă termenii nu cuprind același radical, se lasă sub forma unei sume/diferențe de numere iraționale:
Exemplu: ![]() +
+ ![]() rămâne scris așa.
rămâne scris așa.
Înmulțirea și împărțirea numerelor reale
Dacă a,b ϵ R atunci a·b ϵ R și ![]() ϵ R. (b nenul)
ϵ R. (b nenul)
![]()
Exemplu: ![]()
![]() , b,y nenule.
, b,y nenule.
Exemplu: ![]()
Puterea unui număr real cu expoent întreg:
Dacă a ϵ R, p ϵ Z, atuci ![]() ϵ R.
ϵ R.
(![]() )
)![]() =
= ![]() , a,b ϵ R, b≥0, n ϵ Z.
, a,b ϵ R, b≥0, n ϵ Z.
Exemplu: (![]() )
)![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
(![]() )
)![]() =
= ![]()
Exemplu: ![]()
(![]() )
)![]() = (
= (![]() )
)![]() , a≥0, nϵ N.
, a≥0, nϵ N.
Exemplu: (![]() )
)![]() = (
= (![]() )
)![]()
Raționalizarea numitorului de forma 
![]() , c>0
, c>0
Exemplu: ![]()
Media aritmetică a n numere reale:
![]()
Exemplu:
Un elev are notele 9, 5 și 7 la istorie. Care este media notelor sale?
![]()
Media aritmetică ponderată a n numere reale
![]()
Exemplu:
Într-o firma exista doi angajați cu salariu de 2500 lei, trei au salariul 3000 lei și un angajat are 4000 lei. Determinați salariul mediu din firma respectivă.
![]()
Media geometrică a două numere reale pozitive a și b
![]()
Exemplu:
Media geometrică a numerelor 2 și 4 este:
![]()
Ecuația de forma  , a ϵ R
, a ϵ R
a) Dacă a ϵ R, a< 0, atunci nu există soluții reale.
b) Dacă a ϵ R, a≥0, atunci:
Soluția este: S = {![]() },
},
Exemplu: Ecuația ![]() , are soluțiile:
, are soluțiile:
x = ![]() sau
sau
x = ![]()
Dacă ți-a plăcut materialul cu Operatii cu numere reale, nu uita să dai share paginii. Te aștept și la secțiunea Cursuri la matematică pentru a te înscrie la sesiunile de recapitulare.
