
Acest material despre unghiuri cuprinde următoarele noțiuni: unghiurile adiacente, unghiurile complementare, unghiurile suplementare, bisectoarea unui unghi.
Unghiurile adiacente
Două unghiuri adiacente sunt două unghiuri care au vârf comun, latură comună și celelalte două laturi de o parte și de alta a laturii comune.
Imagine interactivă
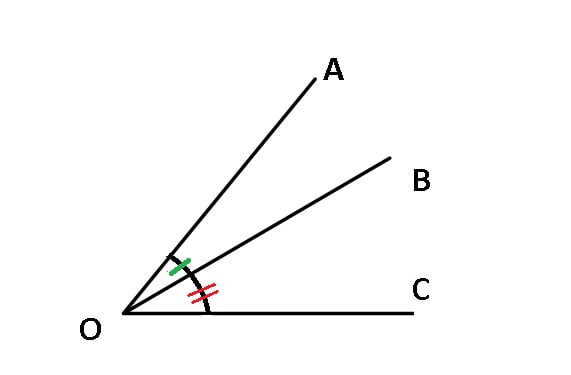
∢AOB și ∢AOC sunt adiacente
m∢AOB + m∢BOC = m∢AOC
m∢AOB = m∢AOC – m∢BOC
m∢BOC = m∢AOC = m∢AOB
Unghiurile complementare
Două unghiuri sunt complementare dacă suma măsurilor lor este 90°.
Exemplu:
m∢A = 30°; m∢B = 60°.
∢A și ∢B sunt complementare pentru că m∢A + m∢B = 30° + 60° = 90°
Complementul unui unghi ∢X este unghiul cu măsura egală cu 90° – m∢X
Exemplu:
Dacă m∢X = 30°, atunci complementul lui ∢X este: 90° – m∢X = 90° – 30° = 60°.
Unghiurile suplementare
Două unghiuri sunt suplementare dacă suma măsurilor lor este 180°.
Exemplu: m∢A = 120°; m∢B = 60°.
∢A și ∢B sunt suplementare pentru că m∢A + m∢B = 120° + 60° = 180°
Suplementul unui unghi ∢X este unghiul cu măsura 180° – m∢X
Exemplu:
Dacă m∢X = 120°, atunci suplementul lui ∢X este: 180° – m∢A = 180° – 120° = 60°.
Bisectoarea unui unghi
Bisectoarea unui unghi este semidreapta cu originea în vârful unghiului, situată în interiorul acestuia și care formează cu laturile acestuia două unghiuri congruente. (Practic, împarte un unghi în două unghiuri cu măsuri egale.)
Imagine interactivă
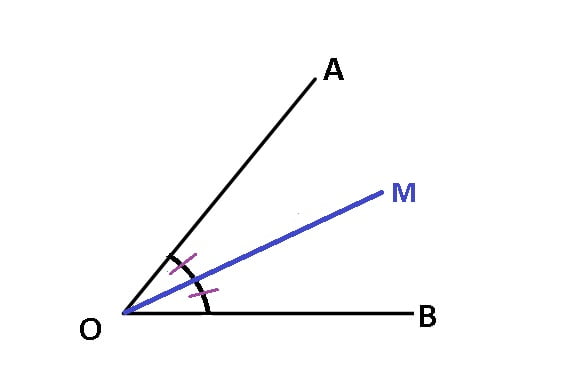
(OM este bisectoarea unghiului ∢AOB ![]() m∢AOM = m∢MOB =
m∢AOM = m∢MOB = ![]()
Exemplu:
Dacă (OM este bisectoarea unghiului ∢AOB și m∢AOB = 60°, atunci:
m∢AOM = m∢MOB = ![]() =
= ![]() = 30°
= 30°
Mai jos puteți viziona un material video privind unghiurile complementare și unghiurile suplementare.
Dacă ți-a plăcut materialul despre Unghiuri, nu uita să dai share paginii. Te aștept și la secțiunea Cursuri la matematică pentru a te înscrie la sesiunile de recapitulare.
