
Acest material despre teorema celor trei perpendiculare cuprinde următoarele noțiuni: teorema celor trei perpendiculare, prima reciprocă a teoremei celor trei perpendiculare, a doua reciprocă a teoremei celor trei perpendiculare.
Teorema celor trei perpendiculare
Fie un plan α, un punct M∉α și o dreaptă d ⊂ α.
Dacă MA ⊥ α, A ∈ α și AB ⊥ d, B ∈ d, atunci MB ⊥ d.
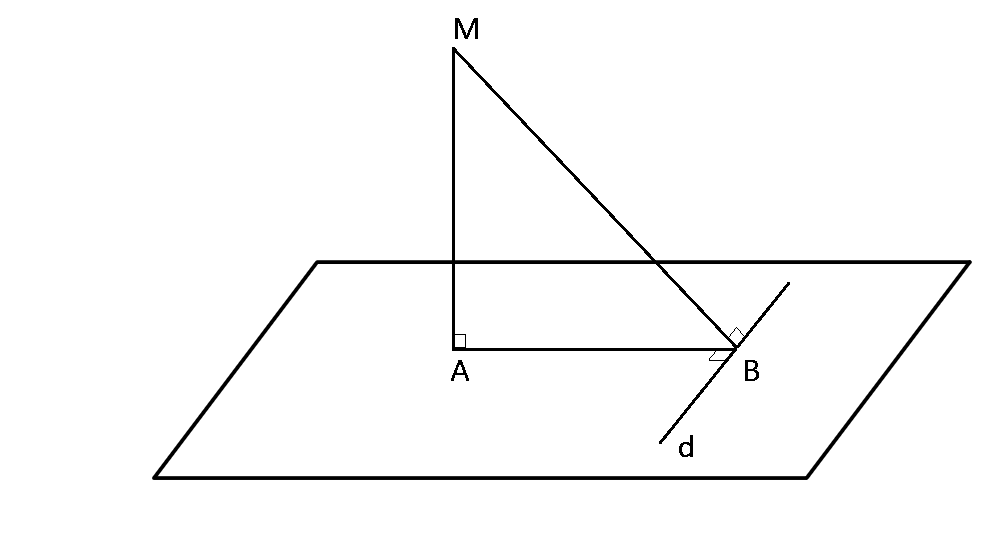
Demonstrație:
MA ⊥ α, dar d ⊂ α, așadar: MA ⊥ d sau d ⊥MA. (Dacă o dreaptă este perpendiculară pe un plan, atunci acea dreaptă este perpendiculară pe orice dreaptă din acel plan).
Dar AB ⊥ d sau d ⊥ AB.
MA ∩ AB = {A}
MA, AB ⊂ (MAB)
Așadar avem d ⊥ (MAB). (Dacă o dreaptă este perpendiculară pe două drepte concurente incluse într-un plan, atunci acea dreaptă este perpendiculară pe acel plan).
MB ⊂ (MAB)
Deci d ⊥ MB sau MB ⊥ d.
Pornind de la teorema celor trei perpendiculare, pot fi formulate două reciproce, ambele adevărate. Cele două teoreme reciproce sunt prezentate în cele ce urmează.
Prima reciprocă a teoremei celor trei perpendiculare
Se consideră un plan α, o dreaptă d ⊂ α și un punct M ∉ α.
Dacă MA ⊥ α, A ∈ α, punctul B ∈ d astfel încât MB ⊥ d, atunci AB ⊥ d.
Cea de-a doua reciprocă a teoremei celor trei perpendiculare
Se consideră un plan α, o dreaptă d ⊂ α, un punct M ∉ α și un punct A ∈ α.
Dacă AB ⊥ d, B ∈ d, MB ⊥ d și MA ⊥ A′B, atunci MA ⊥ α.
Dacă ți-a plăcut materialul despre Teorema celor trei perpendiculare, prima reciprocă și a doua reciprocă a teoremei celor trei perpendiculare, nu uita să dai share paginii. Te aștept și la secțiunea Cursuri la matematică pentru a te înscrie la sesiunile de recapitulare.
