
Acest material despre Relații metrice în triunghiul dreptunghic include următoarele noțiuni: proiecții ortogonale pe o dreaptă, teorema înălțimii, teorema catetei, teorema lui Pitagora, reciproca teoremei lui Pitagora, noțiuni de trigonometrie în triunghiul dreptunghic.
Proiecții ortogonale pe o dreaptă
Proiecția ortogonală a unui punct A pe o dreaptă d reprezintă piciorul perpendicularei duse din punctul A pe dreapta d.
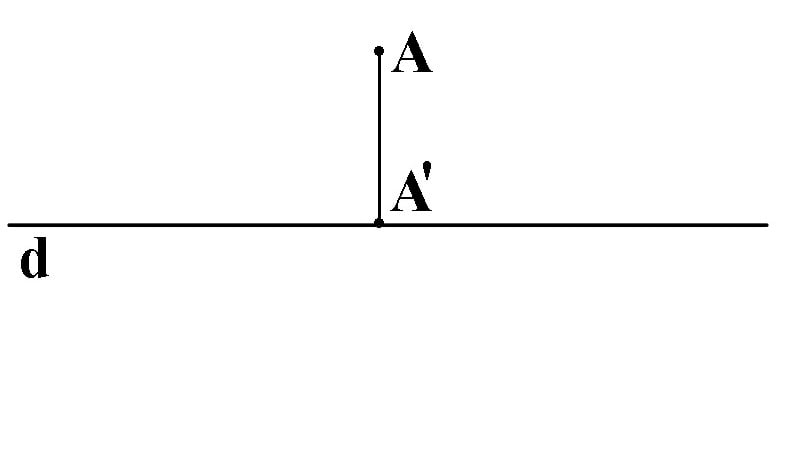
Dacă A ∉ d: prdA=A’, unde AA’⊥d, A’∈ d:
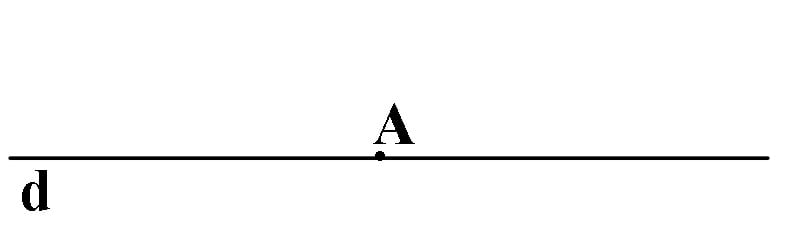
Dacă A ∈ d: prdA=A
Proiecția ortogonală a unui segment AB pe o dreaptă d reprezinta segmentul care cuprinde proiecțiile tuturor punctelor de pe segmentul AB pe dreapta d.
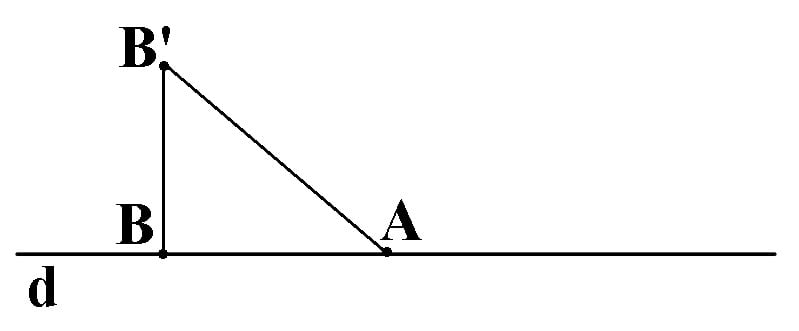
Dacă AB nu este perpendicular pe d, A,B ∉ d, atunci prdAB=A’B’, unde A’= prdA, B’= prdB.
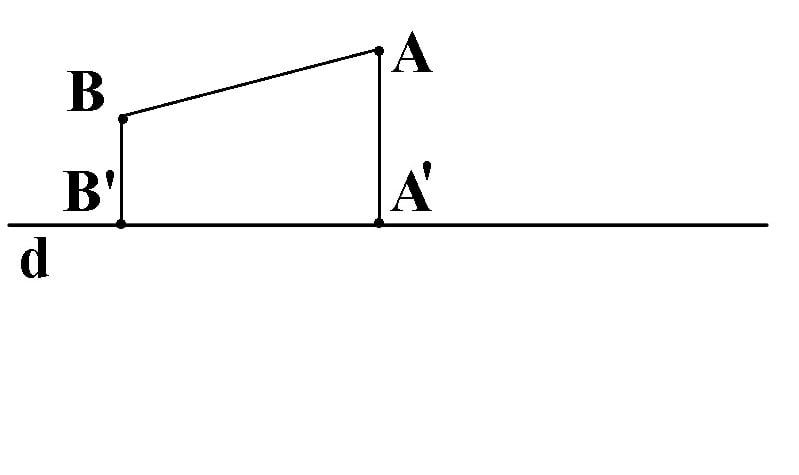
Dacă AB nu este perpendicular pe d, A ∈ d,B ∉ d, atunci prdAB=AB’, unde unde B’= prdB.
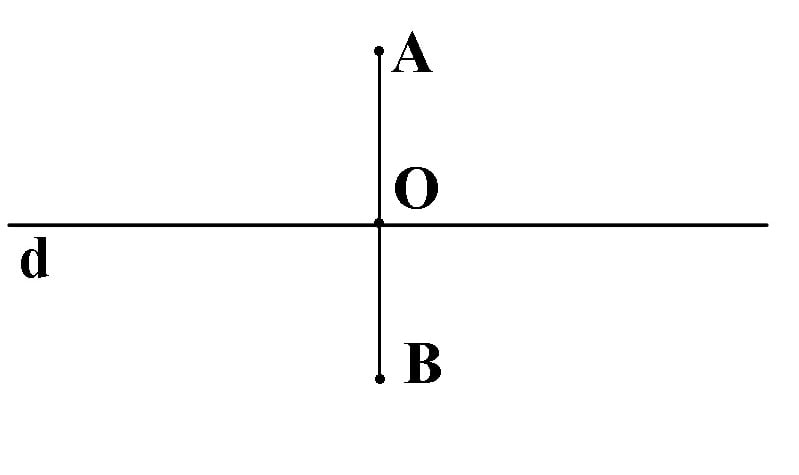
Dacă AB ⊥ d, atunci prdAB=O unde AB ∩ d = {O}.
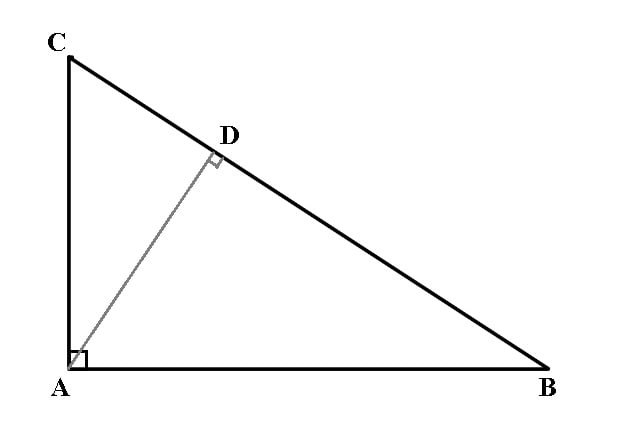
Teorema înălțimii
Într-un triunghi dreptunghic, lungimea înălțimii care pleacă din vârful unghiului drept este medie geometrică între lungimile proiecțiilor catetelor pe ipotenuză.
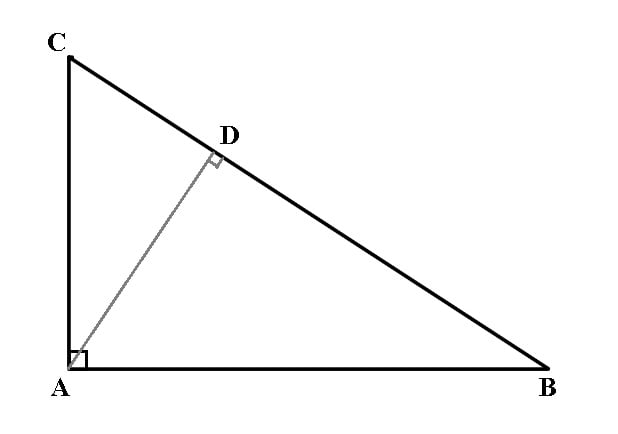
ΔABC cu m∢A = 90°, dacă AD⊥BC, D∈BC, atunci:
AD = ![]() sau
sau
AD2=BD ∙ CD
Reciproca teoremei înălțimii
Dacă într-un triunghi ABC, care nu este triunghi obtuzunghic, lungimea înălțimii AD este media geometrică a lungimilor proiecțiilor laturilor AB și AC pe BC, atunci acel triunghi este dreptunghic.
ΔABC cu m∢A ≤ 90°, m∢B ≤ 90°, m∢C ≤ 90°, dacă AD = ![]() sau AD2=BD ∙ CD, atunci:
sau AD2=BD ∙ CD, atunci:
m∢A = 90°
Teorema catetei
Într-un triunghi dreptunghic, lungimea unei catete este medie geometrică între lungimea ipotenuzei și lungimea proiecției respectivei catete pe ipotenuză.

ΔABC cu m∢A = 90°, dacă AD⊥BC, D∈BC, atunci:
AB = ![]() sau AB2=BC ∙ BD și
sau AB2=BC ∙ BD și
AC = ![]() sau AC2=BC ∙ CD
sau AC2=BC ∙ CD
Reciproca teoremei catetei
Dacă într-un triunghi ABC, cu D=prBCA și D∈B, avem: AB2=BC ∙ BD sau AC2=BC ∙ CD, atunci m∢A = 90°.
Teorema lui Pitagora
Într-un triunghi dreptunghic, pătratul lungimii ipotenuzei este egal cu suma pătratelor lungimilor catetelor.
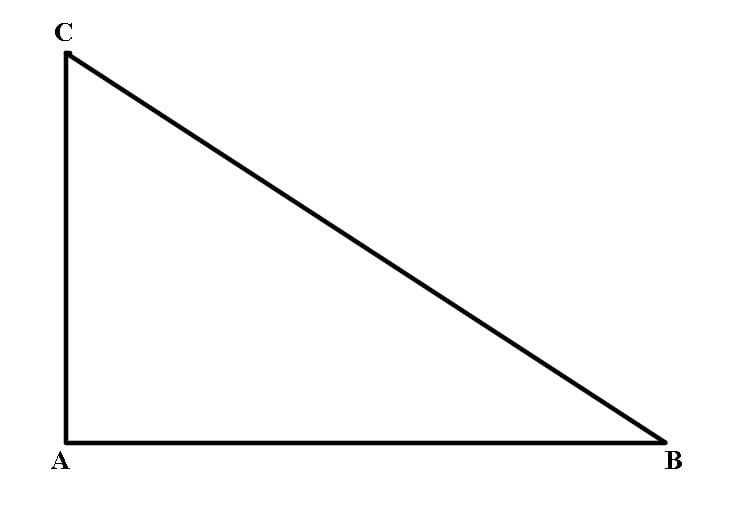
În ΔABC cu m∢A = 90°, BC2 = AB2 + AC2.
Reciproca teoremei lui Pitaora
Dacă, într-un triunghi, pătratul lungimii unei laturi este suma pătratelor celorlalte două laturi, atunci triunghiul este dreptunghic, unghiul drept fiind cel opus primei laturi.
Dacă, într-un triunghi ABC are loc relația BC2 = AB2 + AC2, atunci ΔABC dreptunghic cu m∢A = 90°.
Noțiuni de trigonometrie în triunghiul dreptunghic
Fie ΔABC cu m∢A:

Sinusul unui unghi ascuțit al unui triunghi dreptunghic:
sinus = ![]()
sin B = ![]()
sin C = ![]()
Cosinusul unui unghi ascuțit al unui triunghi dreptunghic:
cosinus = ![]()
cos B = ![]()
cos C = ![]()
Tangenta unui unghi ascuțit al unui triunghi dreptunghic:
tangenta = ![]()
tg B = ![]()
tg C = ![]()
Cotangenta unui unghi ascuțit al unui triunghi dreptunghic:
cotangenta = ![]()
ctg B = ![]()
ctg C = ![]()
| Măsura unghiului: | 30° | 45° | 60° |
| sin: | |||
| cos: | |||
| tg: | 1 | ||
| ctg: | 1 |
Dacă ți-a plăcut materialul despre Relații metrice în triunghiul dreptunghic, nu uita să dai share paginii. Te aștept și la secțiunea Cursuri la matematică pentru a te înscrie la sesiunile de recapitulare.
