Rapoarte și proporții. Material GRATUIT clasa a 6a.

Acest material despre rapoarte și proporții cuprinde următoarele noțiuni: raportul a două numere raționale, proporții, proprietatea fundamentală a proporțiilor, proporții derivate, mărimi direct proporționale, mărimi invers proporționale , regula de trei simplă și probabilități.

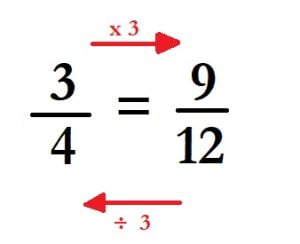
Raportul a două numere raționale

Raportul a două numere raționale a și b (b nenul) este a:b sau $\dfrac{a}{b}$

Proporția

Proporția reprezintă egalitatea dintre două rapoarte:

$\dfrac{a}{b} = \dfrac{c}{d}$

Proprietatea fundamentală a proporțiilor

Dacă $\dfrac{a}{b}=\dfrac{c}{d}$ atunci a⋅d=b⋅c, unde b și d sunt nenule (produsul mezilor=produsul extremilor)

Dacă $\dfrac{a}{b}=\dfrac{c}{d}$ , atunci:

$a= \dfrac{b\cdot c}{d}$

$b= \dfrac{a\cdot d}{c}$

$c= \dfrac{a\cdot d}{b}$

$d= \dfrac{b\cdot c}{a}$

Proporții derivate

Dacă $\dfrac{a}{b}=\dfrac{c}{d}$ atunci:

$\dfrac{d}{b}=\dfrac{c}{a}$

$\dfrac{a}{c}=\dfrac{b}{d}$

$\dfrac{d}{c}=\dfrac{b}{a}$

$\dfrac{c}{d}=\dfrac{a}{b}$

$\dfrac{a+b}{b}=\dfrac{c+d}{d}$

$\dfrac{a-b}{b}=\dfrac{c-d}{d}$

$\dfrac{a}{b+a}=\dfrac{c}{d+c}$

Mărimi direct proporționale

{x,y,z..} și {a,b,c..} sunt direct proporționale dacă:

$\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=$ …=k.

De aici rezultă că:

x=ak;

y=bk;

z=ck;

….

Exemple de mărimi direct proporționale: distanța parcursă și timpul necesar, prețul total al grâului și cantitatea acestuia, etc.

Mărimi invers proporționale

{x,y,z..} și {a,b,c..} sunt invers proporționale dacă:

$\dfrac{x}{\frac{1}{a}}=\dfrac{y}{\frac{1}{b}}=\dfrac{z}{\frac{1}{c}}=$ …=k

<=>

ax = by = cz = … =k

De aici rezultă că:

x= $\dfrac{k}{a}$

y= $\dfrac{k}{b}$

z= $\dfrac{k}{c}$

….

Exemple de mărimi invers proporționale: numărul muncitorilor si nr de ore în care termină o lucrare, debitul unui robinet si timpul în care se umple un bazin cu apă etc.

Regula de trei simplă

Exemplu 1

(mărimi direct proporționale)

Două stilouri de același fel costa 30 lei. Cât costa trei stilouri de același fel?

2 stilouri …….. 30 lei
3 stilouri ………. X lei

X= $\dfrac{30\cdot 3}{2}$ =45 lei

Exemplu 2

(Procente)

10% dintr-un număr este 50. Aflați numărul.

10% …….. 50
100% ………X

X= $\dfrac{50\cdot 100}{10}$ = 500

Exemplu 3

(mărimi invers proporționale)

Cinci muncitori termină o lucrare în 2 ore. În cât timp termină lucrarea 10 muncitori?

5muncitori …….. 2 ore
10 muncitori ….. X ore

X= $\dfrac{5\cdot 2}{10}$ = 1 (o oră)

Probabilități

Probabilitatea este raportul dintre numărul cazurilor favorabile și numărul tuturor cazurilor posibile.

p = $\dfrac{număr cazuri favorabile}{număr cazuri posibile}$

Exemplu:

Într-o urnă sunt 5 bile albe, 3 negre si 2 roșii. Care este probabilitatea de a extrage o bilă neagră?

P = $\dfrac{3}{5+3+2}$ = $\dfrac{3}{10}$

Utilizare

Rapoartele și proporțiile sunt concepte importante în matematică, cu numeroase aplicații în diferite domenii.

În matematică, rapoartele și proporțiile pot fi utilizate pentru a rezolva probleme precum divizarea unui obiect în părți egale sau determinarea relației dintre două mărimi. De asemenea, pot fi folosite pentru a studia concepte precum proporția și raportul de scalare.

În inginerie, rapoartele și proporțiile pot fi utilizate în proiectarea sistemelor mecanice, cum ar fi proporția dintre lungimea și diametrul unei piese sau raportul dintre forța aplicată și rezultanta.

În artă, rapoartele și proporțiile pot fi utilizate pentru a crea compoziții și forme estetice, cum ar fi proporția dintre dimensiunile și distanța dintre elementele unei compoziții.

Dacă ți-a plăcut materialul despre rapoarte și proporții, nu uita să dai share paginii. Te aștept și la secțiunea Cursuri la matematică pentru a te înscrie la sesiunile de recapitulare.