Puteri cu exponent real al unui număr pozitiv 📚 Matematică România

Acest material cuprinde următoarele noțiuni: puteri cu exponent real al unui număr pozitiv, formule de calcul, definiție și aplicare în viața reală.

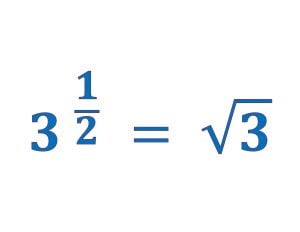
Formule de calcul

1). $a^0=1, \forall a\in\mathbb{R}^*$ ; $0^n=0, \forall n\neq0$

Ex. $5^0=1, \ \ \ \ (\frac{3}{8})^0=1, \ \ \ \ (-\sqrt{3})^0=1$ .

2). $a^n=\underbrace{ a\cdot a\ldots\cdot a}_{\text{de } n \text{ ori}}, \forall a\in\mathbb{R}, n\in\mathbb{N}^*$ (puterea cu exponent natural)

Ex. $5^3=5\cdot 5\cdot 5=125, \ \ \ \ (-\frac{1}{2})^4=(-\frac{1}{2})\cdot (-\frac{1}{2})\cdot(-\frac{1}{2})\cdot (-\frac{1}{2})=\frac{1}{8}$ .

3). $a^{-1}={1 \over a} , \forall a\in\mathbb{R}^*$

Ex. $7^{-1}=\frac{1}{7}$ , $(\frac{3}{2})^{-1}=\frac{2}{3}, \ \ \ \ (\frac{\sqrt 6}{2})^{-1}=\frac{2}{\sqrt{6}}=\frac{2\sqrt{6}}{6}=\frac{\sqrt{6}}{3}$ .

4). $a^{-n}={1\over a^n}, \forall a\in\mathbb{R}^*, n\in\mathbb{N}^*$ (puterea cu exponent întreg)

Ex. $2^{-3}=\frac{1}{2^3}=\frac{1}{8}, \ \ \ \ (-\sqrt{5})^{-4}=\frac{1}{(-\sqrt{5})^{4}}=\frac{1}{\sqrt{625}}=\frac{1}{25}$ .

Reguli de calcul

5). $a^n\cdot a^m=a^{n+m}$ , $\forall a\in\mathbb{R}^*, n,m\in\mathbb{Z}$

Ex. $3^{100}\cdot 3^{50}=3^{100+50}=3^{150}$

$\sqrt{11}^{-17}\cdot \sqrt{11}^{20}=\sqrt{11}^{-17+20}=\sqrt{11}^3=11\sqrt{11}$ .

6). $a^n:a^m=a^{n-m}$ , $\forall a\in\mathbb{R}^*, n,m\in\mathbb{Z}$

Ex. $(-4)^{100}:(-4)^{97}=(-4)^{100-97}=(-4)^{3}=-64$

$2^7:2^{10}=2^{7-10}=2^{-3}=\frac{1}{2^3}=\frac{1}{8}$ .

7). $(a^n)^m=a^{n\cdot m}$ , $\forall a\in\mathbb{R}^*, n,m\in\mathbb{Z}$

Ex. $[(\frac{5}{6})^3]^5=(\frac{5}{6})^{15}, \ \ \ \ (3^4)^{-10}=3^{-40}$ .

8). $(a\cdot b)^n=a^n\cdot b^n$ , $\forall a,b\in\mathbb{R}^*, n\in\mathbb{Z}$

Ex. $(2\sqrt{3})^4=2^4\cdot \sqrt{3}^4=16\cdot 9=144$ .

9). $({a\over b})^n={a^n\over b^n}$ , $\forall a,b\in\mathbb{R}^*, n\in\mathbb{Z}$

Ex. $(\frac{x}{5})^3=\frac{x^3}{125}$ .

Formulele de mai sus au fost aprofundate și în clasele din gimnaziu (puteți accesa lecția AICI ). Vom extinde noțiunea de ridicare la putere astfel:

Definiție:

Fie $a\geq0$ , $n\in\mathbb{N}$ , $n\geq2$ . Numărul real $x$ cu proprietatea că $x^n=a$ se numește puterea cu exponentul rațional ${1 \over n}$ a numărului real pozitiv $a$ și se notează cu $a^{1\over n}$ sau $\sqrt[n]{a}$ .

10). $a^{\frac{1}{n}}=\sqrt[n]{a}, \forall n\in\mathbb{N}, n\geq2, a>0$ .

Ex. $5^{\frac{1}{3}}=\sqrt[3]{5}, \ \ \ \ 10^{\frac{1}{6}}=\sqrt[6]{10}$ .

11). $a^{\frac{m}{n}}=(a^m)^{\frac{1}{n}}=(a^{\frac{1}{n}})^m$ , $\forall n\in\mathbb{N}, n\geq2, m\in\mathbb{Z}, a>0$ .

Dacă bazele $a$ și $b$ sunt strict pozitive ( $a>0, b>0$ ), atunci formulele 3).-9). sunt valabile și pentru exponenți raționali sau reali.

Ex. Scrieți sub formă de putere rezultatul

$(2^{20}\cdot 4^{15}:\sqrt{8}^5)^{\frac{3}{2}}=[2^{20}\cdot (2^2)^{15}:(8^{\frac{1}{2}})^5]^{\frac{3}{2}}=[2^{20}\cdot 2^{30}:(2^3)^{\frac{5}{2}}]^{\frac{3}{2}}=$

$=(2^{50}:2^{\frac{15}{2}})^{\frac{3}{2}}=(2^{\frac{85}{2}})^{\frac{3}{2}}=2^{\frac{255}{4}}$ .

Utilizare în viața de zi cu zi: Puteri cu exponent real al unui număr pozitiv

Puterile cu exponent real ale unui număr pozitiv reprezintă un concept matematic fundamental cu numeroase aplicații practice în viața de zi cu zi. În ceea ce urmează, vom explora câteva dintre avantajele utilizării puterilor cu exponent real ale unui număr pozitiv în contextul real și impactul asupra diferitelor aspecte ale vieții noastre.

Tehnologia și calculul științific: Puterile cu exponent real sunt esențiale în domeniul calculului științific și tehnologiei avansate. Algoritmi de învățare automată și inteligență artificială se bazează pe operarea cu puteri ale numerelor pozitive pentru a procesa și interpreta datele. Prin utilizarea puterilor cu exponent real, cercetătorii pot modela și prezice fenomene complexe în diverse domenii, cum ar fi meteorologia, economia și biologia.
Finanțe personale și investiții: În lumea finanțelor personale, puterile cu exponent real joacă un rol crucial în calculul ratelor dobânzilor compuse. Acestea permit oamenilor să estimeze evoluția economiilor personale în timp și să ia decizii informate privind economisirea și investițiile. Astfel, înțelegerea conceptului de exponent real este esențială pentru gestionarea responsabilă a banilor și construirea unui viitor financiar stabil.
Industria energetică și ecologie: În sectorul energetic, puterile cu exponent real sunt folosite pentru a analiza ratele de creștere a cererii de energie, a producției de energie regenerabilă și a consumului de resurse naturale. Prin înțelegerea acestei noțiuni matematice, specialiștii în domeniul energiei pot optimiza distribuția și utilizarea resurselor, contribuind la sustenabilitatea și protecția mediului.
Construcții și inginerie: În domeniul construcțiilor și ingineriei, puterile cu exponent real sunt esențiale în calculul rezistenței materialelor și a structurilor. Aceste cunoștințe permit proiectarea și construcția de edificii solide, durabile și sigure, având un impact semnificativ asupra siguranței și confortului oamenilor.Concluzie: Puterile cu exponent real ale unui număr pozitiv au o importanță imensă în lumea noastră modernă și sunt utilizate în numeroase domenii, de la știință și tehnologie până la finanțe personale și inginerie.

Concluzie:

Puterile cu exponent real ale unui număr pozitiv au o importanță imensă în lumea noastră modernă și sunt utilizate în numeroase domenii, de la știință și tehnologie până la finanțe personale și inginerie. Înțelegerea și aplicarea acestui concept matematic ne permit să luăm decizii informate, să prognozăm tendințe și să contribuim la progresul societății în multiple moduri. Indiferent dacă suntem conștienți sau nu, puterile cu exponent real fac parte din viața noastră cotidiană și ne influențează în mod pozitiv în multiple aspecte.

Dacă ți-a plăcut materialul despre Puteri cu exponent real al unui număr pozitiv, nu uita să dai share paginii. Te aștept și la secțiunea Cursuri la matem atică pentru a te înscrie la sesiunile de recapitulare.