
Acest material despre perpendicularitate cuprinde următoarele noțiuni: drepte perpendiculare, dreaptă perpendiculară pe plan, distanța de la un punct la un plan, distanța dintre două plane paralele, plane perpendiculare. Perpendicularitatea a fost studiată și în clasa a 6-a.
Drepte perpendiculare
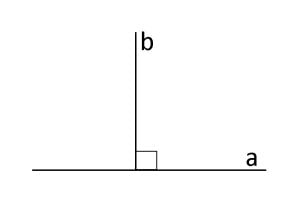
Două drepte sunt perpendiculare dacă formează un unghi drept.
a Ʇ b ⇔ m∠(a, b) = 90⁰.
Dreaptă perpendiculară pe plan
Definiție: O dreaptă perpendiculară pe un plan este o dreaptă perpendiculară pe orice dreaptă din acel plan.
O dreaptă este perpendiculară pe un plan, dacă este perpendiculară pe două drepte concurente din acel plan.
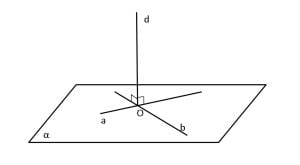
Dacă:
d⟂a, a ⊂ α
d⟂b, b ⊂ α
a∩b={O}
Atunci: d⟂α
O dreaptă este perpendiculară pe un plan dacă este paralelă cu o dreaptă perpendiculară pe acel plan.
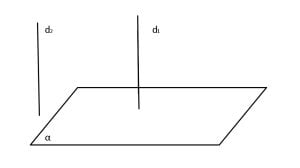
Dacă:
d1⟂α
d2 || d1
Atunci:
d2⟂α
Distanța de la un punct la un plan
Distanța de la un punct la un plan reprezintă lungimea segmentului dintre acel punct și piciorul perpendicularei dusă din acel punct pe plan.
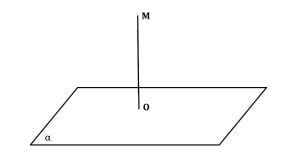
d(M; α) = MO, unde MO⟂α, iar MO ∩α={O}.
Distanța dintre două plane paralele
Distanța dintre două plane paralele reprezintă distanța de la un punct al unuia la celălalt plan.
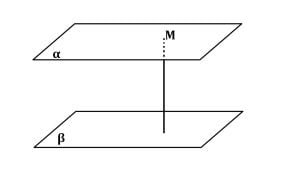
d(α, β) = d(M, β) unde M∈α.
Plane perpendiculare
Dacă un plan conține o dreaptă perpendiculară pe alt plan, atunci cele două plane sunt perpendiculare.
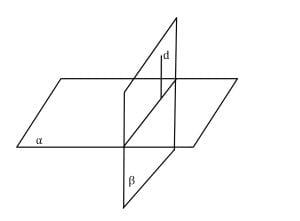
Dacă:
d⟂α
d ⊂ α
Atunci:
α ⟂ β
Utilizare
Perpendicularitatea este un concept important în geometrie, cu numeroase aplicații în diferite domenii.
În matematică, perpendicularitatea poate fi utilizată pentru a studia proprietățile figurilor geometrice, cum ar fi dreptunghiurile, trapezii și paralelogramele. De asemenea, poate fi folosită pentru a rezolva probleme matematice precum proiectarea sistemelor de coordonate și calcularea unghiurilor între două linii sau planuri.
În inginerie, perpendicularitatea poate fi folosită în proiectarea structurilor, cum ar fi construcțiile de clădiri și poduri. De asemenea, poate fi utilizată în proiectarea sistemelor de navigație, cum ar fi radarul și sateliții.
În artă, perpendicularitatea poate fi utilizată pentru a crea compoziții și forme, cum ar fi linii drepte și unghiuri în desen sau sculptură.
În concluzie, perpendicularitatea are aplicații multiple în matematică, inginerie, artă și alte domenii.
Dacă ți-a plăcut materialul despre perpendicularitate, nu uita să dai share paginii. Te aștept și la secțiunea Cursuri la matematică pentru a te înscrie la sesiunile de recapitulare.
