
Acest material despre geometrie în spațiu – noțiuni introductive, cuprinde următoarele informații: noțiuni de bază privind puncte, drepte și plane, determinarea planului și pozițiile relative a două drepre în spațiu.
Noțiuni de bază privind puncte, drepte și plane
- Prin două puncte distincte trece o dreaptă și numai una.
A ≠ B; A,B ϵ d => AB=BA=d

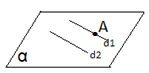
- Într-un plan, printr-un punct exterior unei drepte, se poate duce o paralelă și numai una la dreapta dată. Oricare două drepte paralele sunt coplanare. (adică se află în același plan)
Dacă A∉d2, există o unică dreaptă d1, pentru care A ϵ d1 și d1||d2
d1 ⸦ α și d2 ⸦ α.
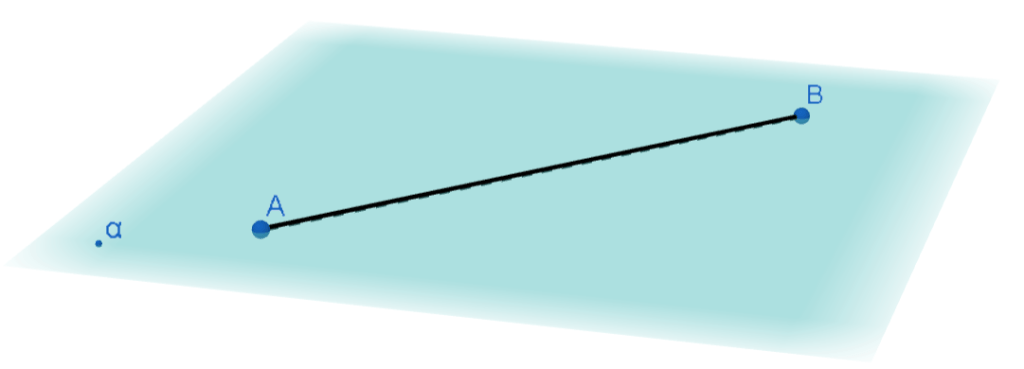
- Dacă două puncte distincte aparțin unui plan, atunci și dreapta determinată de acele puncte este inclusă în acel plan.
Dacă A ϵ α și B ϵ α, A≠B, atunci AB ⸦ α.
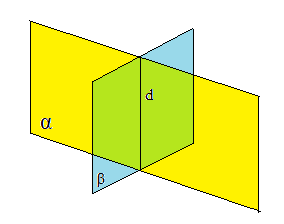
- Dacă două plane se intersectează, intersecția lor este o dreaptă.
α ∩ ꞵ = {d}.
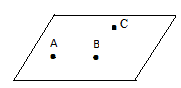
Determinarea planului
- Trei puncte necoliniare determină un plan: Dacă A,B,C necoliniare, putem determina planul (ABC).
- O dreaptă și un punct exterior ei determină un plan: Dacă A∉d, atunci putem determina planul (A,d)
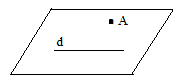
- Două drepte concurente determină un plan: Dacă d1∩d2={O}, atunci putem determina planul (d1,d2)
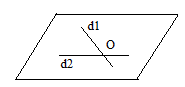
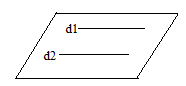
- Două drepte paralele determină un plan: Dacă d1||d2, atunci putem determina planul (d1,d2)
Pozițiile relative a două drepte în spațiu
- Drepte concurente = sunt coplanare și se intersectează într-un punct: d1∩d2={O}, d1,d2⸦ α
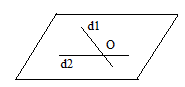
- Drepte paralele = sunt coplanare și nu au niciun punct comun: d1 | | d2; d1,d2⸦ α
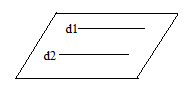
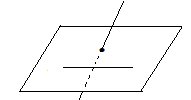
- Drepte necoplanare = nu sunt incluse în același plan, nu sunt paralele, dar nici concurente
Dacă ți-a plăcut materialul, nu uita să dai share paginii. Te aștept și la secțiunea Cursuri la matematică pentru a te înscrie la sesiunile de recapitulare.
