Funcții📚

Acest material despre funcții cuprinde următoarele noțiuni: noțiunea de funcție, imaginea unei funcții, graficul unei funcții și funcții numerice, funcții de forma f : D → ℝ, f(x) = ax +b, unde a, b ∈ ℝ, iar D ⊂ ℝ sau D = ℝ reprezentarea grafică a unei funcții de forma f : ℝ → ℝ, f(x) = ax +b, unde a, b ∈ ℝ

Noțiunea de funcție

Fie două mulțimi nevide A și B. Dacă, printr-un procedeu oarecare, îi atribuim fiecărui element din mulțimea A un singur element din mulțimea B, spunem că definim funcția f pe mulțimea A cu valori în mulțimea B.

Notație:

f : A → B (citim: funcția f, definită pe A cu valori în B)

Mulțimea A se numește: domeniu de definiție

Mulțimea B se numește: codomeniu (mulțimea în care ia valori funcția)

Procedeul f se numește: lege de coresondență

Dacă unui element x din mulțimea A îi corespunde un unic element y din mulțimea B, printr-o lege de corespondență f, spunem ca valoarea funcției f în x este y și scriem: f(x)=y.

În funcție de modalitatea în care este dată legea de corespondență, o funcție poate fi reprezentată prin:

Diagrama;
Tabel;
O expresie algebrică
Mai multe expresii algebrice

Exemplificăm mai jos:

Diagramă:

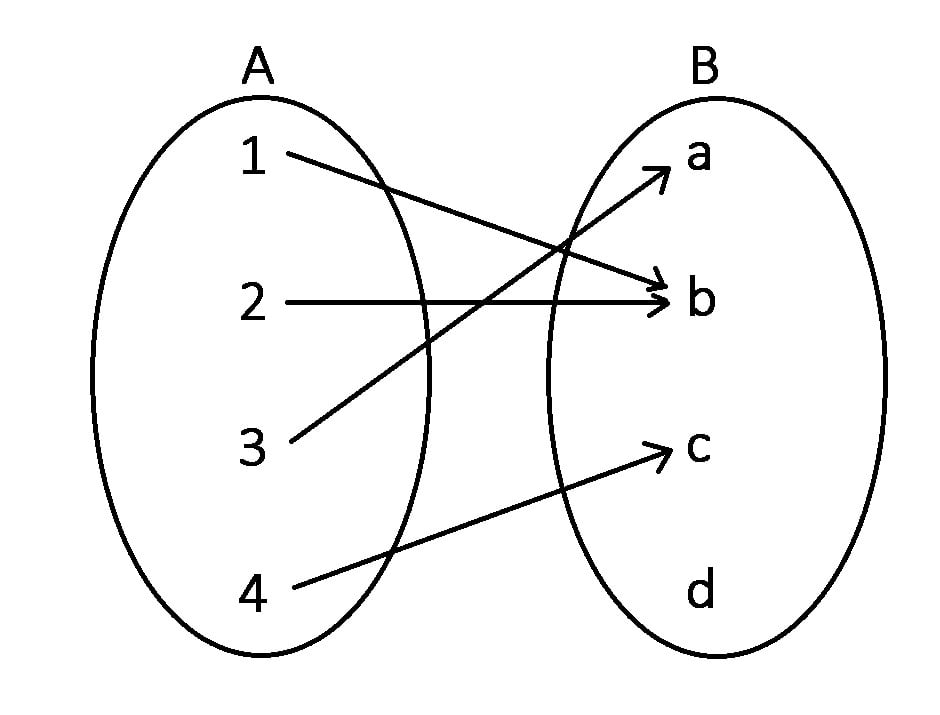
Tabel:

x	2	3	5	7
f(x)	4	6	10	14

Expresie algebrică:

f : ℝ → ℝ

f(x) = 5x + 3

Mai multe expresii algebrice:

f : ℝ → ℝ

f(x) = 2x, pentru x ∈ ( -∞, 0)

f(x) = 3x – 1, pentru x ∈ [0, +∞)

Imaginea unei funcții

Fie f : A → B

Imaginea funcției f reprezintă mulțimea tuturor valorilor pe care le poate lua funcția f și se notează Imf.

Imf = {f(x) | x ∈ A}

Exemplu:

f : {1,2,3} → ℝ

f(x) = x+1

f(1) = 1+1 = 2

f(2) = 2+1 = 3

f(3) = 3+1 = 4

Așadar Imf = {2,3,4}

Graficul unei funcții. Funcții numerice

Graficul unei funcții f : A → B se notează Gf și reprezintă mulțimea definită astfel:

Gf = {(x, y), x ∈ A, y ∈ B, y = f(x)}

O funcție f : A → B este o funcție numerică dacă toate elementele din A și B sunt numere reale.

Altfel spus, f : A → B este o funcție numerică dacă A ⊂ ℝ și B ⊂ ℝ sau A = B = ℝ.

Exemplu de funcție numerică:

f : (1,2) → ℝ, f(x) = x+1.

Reprezentarea geometrică a graficului funcției f constă în mulțimea tuturor punctelor de coordonate x și y, unde f(x) = y.

Exemplu:

f : {1,3} → ℝ;

f(1) = -2,

f(3) = 2.

Avem Gf = {A(1,-2), B(3,2)}

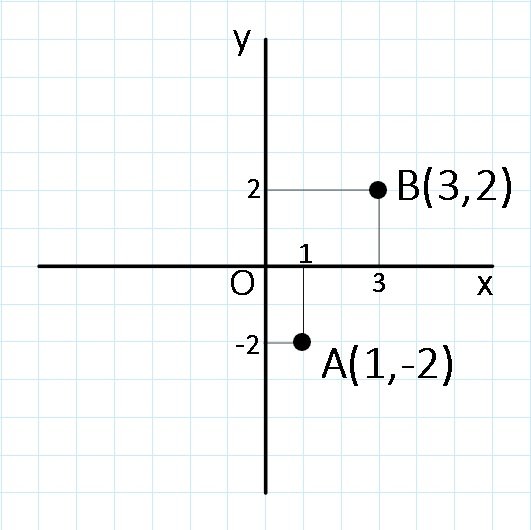
Funcții de forma f : D → ℝ, f(x) = ax + b, unde a, b ∈ ℝ, iar D ⊂ ℝ sau D = ℝ

Fie f : ℝ → ℝ, f(x) = ax + b. a,b ∈ ℝ.

Dacă a=0, atunci f(x) = b și f este o funcție constantă.

Exemplu de funcție constantă: f : ℝ → ℝ, f(x) = -3.

Dacă a≠0, atunci f(x) = ax + b și f este o funcție de gradul I.

Exemplu de funcție de gradul I: f : ℝ → ℝ, f(x) = 2x – 4.

Reprezentarea grafică a funcției de forma f : ℝ → ℝ, f(x) = ax + b, unde a, b ∈ ℝ

Graficul unei funcții de forma f : ℝ → ℝ, f(x) = ax + b, unde a, b ∈ ℝ este o dreaptă.

Modalități de reprezentare a graficului unei funcții de forma f : ℝ → ℝ, f(x) = ax + b, unde a, b ∈ ℝ

Identificarea a două puncte distince, aleatorii, de pe graficul funcției f.
Identificarea punctelor reprezentând intersecția graficului funcției f cu axele de coordonate din sistemul xOy.

Exemplu:

f : ℝ → ℝ, f(x) = 2x – 4

Modalitatea 1: Identificarea a două puncte distince, aleatorii, de pe graficul funcției f.

Alegem, în mod aleatoriu, două valori pentru x:

Pentru x = 1:

f(1) = 2⋅ 1 – 4

f(1) = -2.

Avem punctul A(1,-2).

Pentru x = 3:

f(3) = 2⋅ 3 – 4

f(3) = 2.

Avem punctul B(3,2).

Reprezentăm punctele A și B în sistemul de coordonate xOy.

Graficul funcției f este dreapta care trece prin punctele A și B.

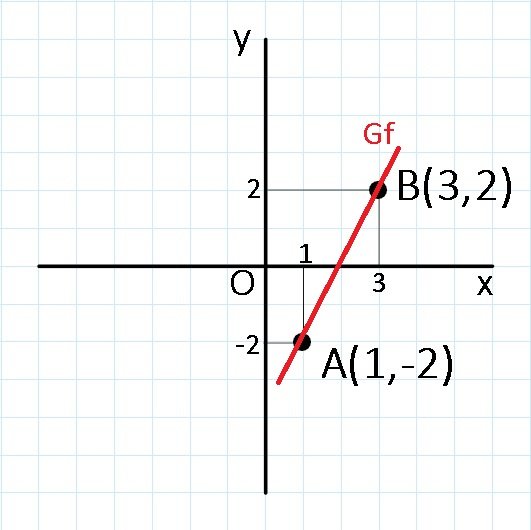
Modalitatea 2: Identificarea punctelor reprezentând intersecția graficului funcției f cu axele de coordonate din sistemul xOy

Pentru intersecția graficului funcției f cu axa de coordonate Ox, se egalează f(x) cu 0 și se calculează x.

Gf ∩ Ox:

f(x) = 0

2x – 4 = 0

Deci 2x – 4 = 0

Obținem x = 2.

Așadar f(2) = 0. Avem punctul A(2,0).

Pentru intersecția graficului funcției f cu axa de coordonate Oy, se egalează x cu 0 și se calculează f(0).

Gf ∩ Oy:

x = 0

f(0) = 2⋅ 0 – 4

Așadar f(0) = -4. Avem punctul B(0,-4).

Graficul funcției f este dreapta care trece prin punctele A și B.

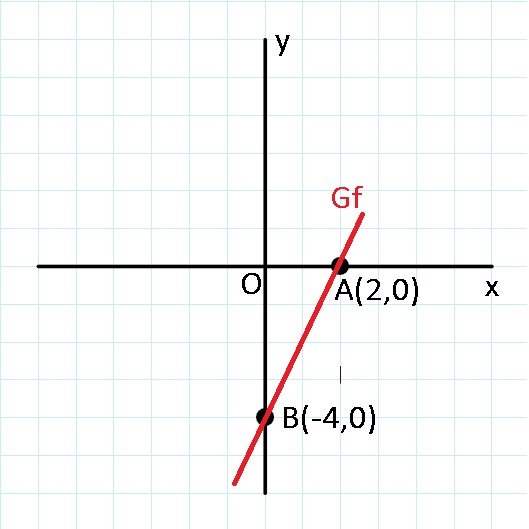
Cum verificăm dacă un punct aparține graficului unei funcții?

Punctul M(m,n) se află pe graficul funcției f : ℝ → ℝ, f(x) = ax + b, unde a, b ∈ ℝ, dacă f(m) = n.

Exemple:

f : ℝ → ℝ, f(x) = x + 5.

Punctul M(2,7) ∈ Gf pentru că f(2) = 2+5 = 7.

Punctul N(-1,-4) ∉ Gf, pentru că f(-1) = -1+5 = 4 ≠ -4.

Reprezentarea graficului unei funcții de forma f : D → ℝ, f(x) = ax + b, unde a, b ∈ ℝ, D ⊂ ℝ

Pentru a reprezenta grafic o funcție f : [p,q] → R, f(x) = ax + b, unde a, b ∈ ℝ, trebuie reprezentate grafic punctele P(p, f(p)) și Q(q, f(q)). Graficul funcției va fi segmentul PQ. Punctele P și Q aparțin graficului funcției.

Pentru a reprezenta grafic o funcție f : [p,q) → R, f(x) = ax + b, unde a, b ∈ ℝ, trebuie reprezentate grafic punctele P(p, f(p)) și Q(q, f(q)). Graficul funcției va fi segmentul PQ. Punctul P aparține graficului funcției, iar punctul Q nu aparține graficului funcției.

Pentru a reprezenta grafic o funcție f : (p,q] → R, f(x) = ax + b, unde a, b ∈ ℝ, trebuie reprezentate grafic punctele P(p, f(p)) și Q(q, f(q)). Graficul funcției va fi segmentul PQ. Punctul P nu aparține graficului funcției, iar punctul Q aparține graficului funcției.

Pentru a reprezenta grafic o funcție f : (p,q) → R, f(x) = ax + b, unde a, b ∈ ℝ, trebuie reprezentate grafic punctele P(p, f(p)) și Q(q, f(q)). Graficul funcției va fi segmentul PQ. Punctele P și Q nu aparțin graficului funcției.

Pentru a reprezenta grafic o funcție f : [p,+∞) → R, f(x) = ax + b, unde a, b ∈ ℝ, trebuie reprezentate grafic punctul P(p, f(p)) și încă un punct Q(q, f(q)). Graficul funcției va fi semidreapta (PQ. Punctele P și Q aparțin graficului funcției.

Pentru a reprezenta grafic o funcție f : (p,+∞) → R, f(x) = ax + b, unde a, b ∈ ℝ, trebuie reprezentate grafic punctul P(p, f(p)) și încă un punct Q(q, f(q)). Graficul funcției va fi semidreapta (PQ. Punctul P nu aparține graficului funcției, iar Q aparține graficului funcției.

Pentru a reprezenta grafic o funcție f : (-∞, q] → R, f(x) = ax + b, unde a, b ∈ ℝ, trebuie reprezentate grafic un punct P(p, f(p)) și punctul Q(q, f(q)). Graficul funcției va fi semidreapta (QP. Punctele P și Q aparțin graficului funcției.

Pentru a reprezenta grafic o funcție f : (-∞, q)→ R, f(x) = ax + b, unde a, b ∈ ℝ, trebuie reprezentate grafic punctul P(p, f(p)) și încă un punct Q(q, f(q)). Graficul funcției va fi semidreapta (PQ. Punctul P aparține graficului funcției, iar Q nu aparține graficului funcției.

Exemplu:

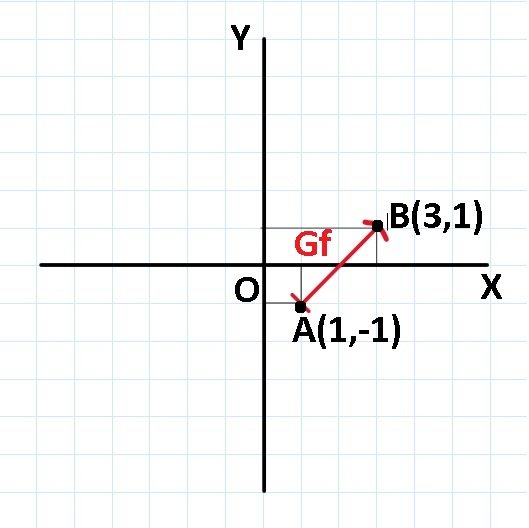
f : [1,3) → R, f(x) = x – 2.

f(1) = -1, deci avem P(1, -1)

f(3) = 1, deci avem Q(3, 1).

Graficul funcției f este segmentul PQ. P aparține graficului funcției, Q nu aparține graficului funcției.

Dacă ți-a plăcut materialul despre Funcții, nu uita să dai share paginii. Te aștept și la secțiunea Cursuri la matematică pentru a te înscrie la sesiunile de recapitulare.