Cercul – noțiuni de bază, acest material despre cerc cuprinde următoarele noțiuni: definiția cercului, rază, coardă, diametru, arc, semicerc, unghi la centru, pozițiile unei drepte față de un cerc și pozițiile relative a două cercuri. Noțiuni avansate despre cerc veți învăța și în clasa a 7-a.
Cercul – noțiuni de bază
Cercul reprezintă totalitatea punctelor egal depărtate de un punct fix, numit centrul cercului.
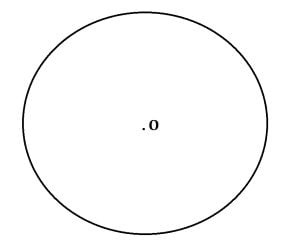
În cercul de mai sus, O este centrul cercului.
Raza cercului:
Distanța de la centrul cercului la orice punct de pe cerc este constantă și se numește rază.
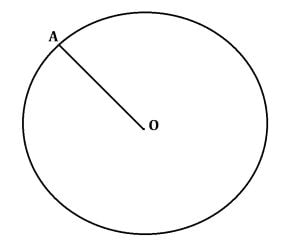
În cercul de mai sus, OA este rază a cercului, unde O = centrul cercului și A este un punct pe cerc.
Coarda și diametrul:
Segmentul care unește două puncte de pe cerc se numește coardă.
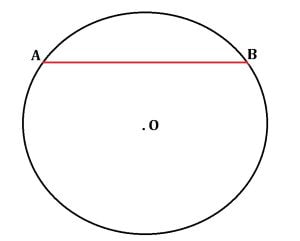
În cercul de mai sus, segmentul AB, evidențiat cu roșu, este coardă, unde A și B sunt două puncte aflate pe cerc.
Coarda care trece prin centrul cercului se numește diametru.
Lungimea diametrului este dublul lungimii unei raze: D = 2R
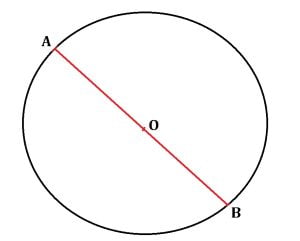
În cercul de mai sus, AB este diametru, unde AB este o coardă, iar punctul O, care este centrul cercului, se află pe coarda AB.
Punctele A și B sunt diametral opuse.
Arcul de cerc și semicercul:
Porțiunea de cerc, cuprinsă între capetele unei coarde se numește arc de cerc.
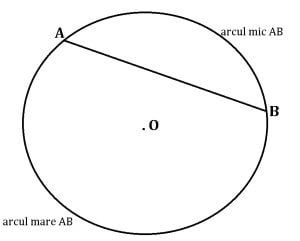
În cercul din imagine, porțiunea de cerc, cea mai scurta, cuprinsă între punctele A și B (puncte aflate pe cerc) reprezintă arcul mic 
, iar porțiunea de cerc, cea mai lunga, cuprinsă între punctele A și B reprezintă arcul mare .
Un arc de cerc cuprins între două puncte diametral opuse se numește semicerc.
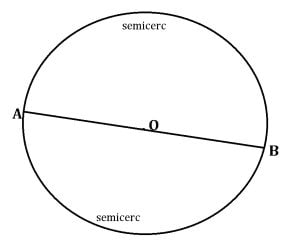
În cercul de mai dus, segmentul AB este diametru, iar arcul este semicerc. Un semicerc are măsura de 180°.
Măsura unui cerc este de 360°.
Unghiul la centru
Un unghi la centru este unghiul care are vârful în centrul unui cerc.
Măsura unui unghi la centru este egală cu măsura arcului cuprins între laturile acestuia.
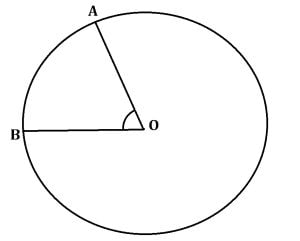
În cercul de mai sus, O este centrul cercului, iar A și B două puncte pe cerc. Unghiul AOB este un unghi la centru.
Pozițiile unei drepte față de un cerc
Dacă o dreaptă are două puncte comune cu un cerc, atunci acea dreaptă este secantă la cerc.
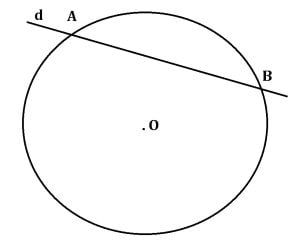
În figura de mai sus, dreapta d intersecteaza cercul în punctele A și B, așadar, dreapta d este secantă la cerc.
Dacă o dreaptă are un punct comun cu un cerc, atunci dreapta este tangentă la cerc.
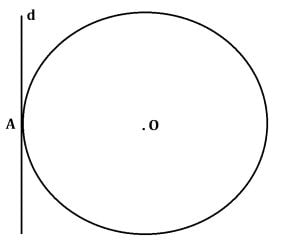
În figura de mai sus, dreapta d intersectează cercul într-un singur punct A, așadar dreapta d este tangentă la cerc.
Dacă o dreaptă nu are niciun punct comun cu cercul atunci dreapta este exterioară cercului.
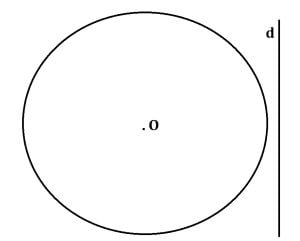
În figura de mai sus, dreapta d și cercul nu au niciun punct comun, așadar, dreapta d este exterioară cercului.
Pozițiile relative a două cercuri
Două cercuri care au două puncte comune sunt cercuri secante:
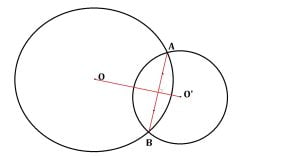
În figura de mai sus, cele două cercuri de centre O, respectiv O’ se intersectează în punctele A și B, așadar cele două cercuri sunt secante.
OO‘ este mediatoarea lui AB.
Două cercuri care au un punct comun se numesc cercuri tangente.
Dacă două cercuri sunt tangente exterioare, distanța dintre centrele lor este egală cu suma razelor celor două cercuri.
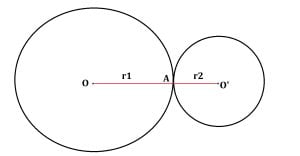
În figura de mai sus, cercurile de centre O, respectiv O’ se intersectează în punctul A, iar cele două cercuri sunt tangente exterioare.
OA = r1 este raza primului cerc, iar O’A=r2 este raza celui de-al doilea cerc.
Avem: OO’ = r1 + r2
Dacă două cercuri sunt tangente interioare, distanța dintre centrele lor este egală cu diferență razelor celor două cercuri.
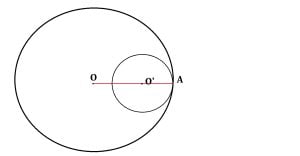
În figura de mai sus, cercurile de centre O, respectiv O’ se intersectează în punctul A, iar cele două cercuri sunt tangente interioare.
OA = r1 este raza primului cerc, iar O’A=r2 este raza celui de-al doilea cerc.
Avem: OO’ = r1 – r2
Dacă ți-a plăcut materialul Fracții ordinare, nu uita să dai share paginii. Te aștept și la secțiunea Cursuri la matematică pentru a te înscrie la sesiunile de recapitulare.
