Arii și volume ale prismelor 📚 Clasa a 8-a.

Acest material despre arii și volume ale prismelor include următoarele noțiuni: prisma triunghiulară regulată, prisma patrulateră regulată, prisma hexagonală regulată, paralelipipedul dreptunghic, cubul.

Aria totală a unei prisme poate fi calculată prin adunarea tuturor suprafețelor sale laterale și a celor două baze. Acest lucru este util într-o serie de domenii, cum ar fi în arhitectură, construcții și design de interior. În arhitectură și construcții, calculul ariei prismelor este important pentru determinarea cantității de material necesar pentru a acoperi pereții exteriori ai clădirilor. În designul de interior, aceste calcule sunt importante în stabilirea dimensiunilor mobilei și a altor obiecte de mobilier care sunt amplasate într-o cameră.

De asemenea, volumul prismelor poate fi calculat utilizând formula specifică care implică înmulțirea suprafeței bazei cu înălțimea prismei. Acest calcul este important în diverse domenii, cum ar fi în inginerie și arhitectură, unde este necesar să se determine capacitatea unui rezervor prismatic sau a unei structuri arhitecturale.

În plus, prismele sunt importante în geometria tridimensională și sunt utilizate frecvent în probleme de matematică pentru a-i ajuta pe elevi să înțeleagă conceptele de suprafață și volum. În general, învățarea despre proprietățile geometrice ale prismelor ajută la dezvoltarea abilităților de gândire spațială și la înțelegerea conceptelor matematice abstracte.

În concluzie, aria și volumul prismelor sunt importante într-o gamă largă de domenii, de la arhitectură și construcții la inginerie și matematică.

Prisma triunghiulară regulată

Aria bazei: A_b = $\dfrac{l^2\sqrt{3}}{4}$

Perimetrul bazei: P_b= 3l

Aria laterală: Al = $Pb \cdot h$ (h=înălțimea prismei)

Aria totală: At = 2Ab + Al;

Volumul: V = $Ab\cdot h$ (h=înălțimea prismei)

Prisma patrulateră regulată

Aria bazei: A_b = $l^2$

Perimetrul bazei: P_b= 4l

Aria laterală: Al = $Pb \cdot h$ (h=înălțimea prismei)

Aria totală: At = 2Ab + Al;

Volumul: V = $Ab\cdot h$ (h=înălțimea prismei)

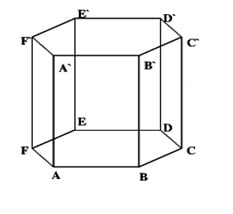
Prisma hexagonală regulată

Aria bazei: A_b = $\dfrac{3l^2\sqrt{3}}{2}$

Perimetrul bazei: P_b= 6l

Aria laterală: Al = $Pb \cdot h$ (h=înălțimea prismei)

Aria totală: At = 2Ab + Al;

Volumul: V = $Ab\cdot h$ (h=înălțimea prismei)

Paralelipipedul dreptunghic

Aria bazei: A_b = $L \cdot l$

Perimetrul bazei: P_b= 2(L+l)

Aria laterală: Al = $Pb \cdot h$

Aria totală: At = 2Ab + Al;

Volumul: V = $Ab\cdot h$ sau V = $L \cdot l \cdot h$

Cubul

Aria bazei: A_b = $l^2$

Perimetrul bazei: P_b= 4l

Aria laterală: Al = $4l^2$

Aria totală: At = $6l^2$

Volumul: V = $l^3$

Dacă ți-a plăcut materialul despre Arii și volume ale prismelor, nu uita să dai share paginii. Te aștept și la secțiunea Cursuri la matem atică pentru a te înscrie la sesiunile de recapitulare.