
Acest material despre proiecții ortogonale în spațiu cuprinde următoarele noțiuni: proiecția unui punct pe un plan, proiecția unei drepte pe un plan, unghiul dintre o dreaptă și un plan, unghiul diedru și unghiul dintre două plane.
Proiecția unui punct pe un plan
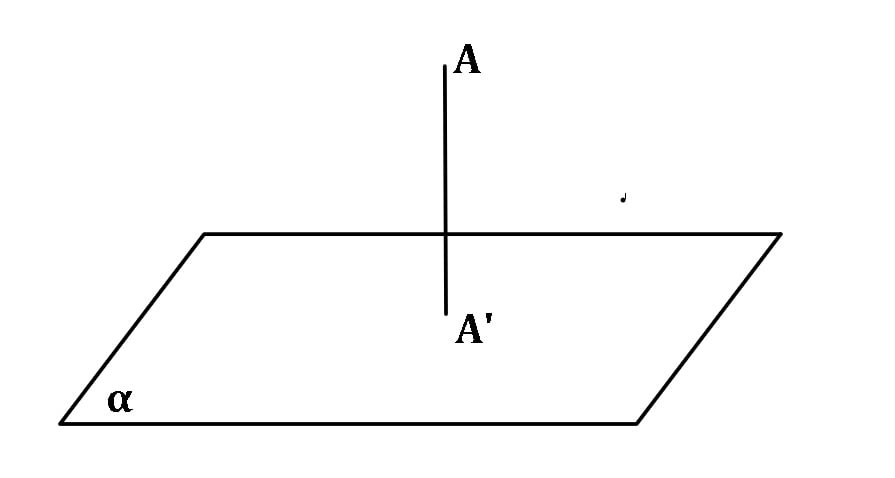
Proiecția unui punct A pe un plan α este punctul de intersecție al perpendicularei din A pe α cu planul α.
prαA = A’, unde AA’⊥ α, AA’∩α = {A’}, A∉α
Proiecția unei drepte pe un plan
Proiecția unei drepte pe un plan este:
- un punct, dacă dreapta este perpendiculară pe plan
- o dreaptă, dacă dreapta nu este perpendiculară pe plan
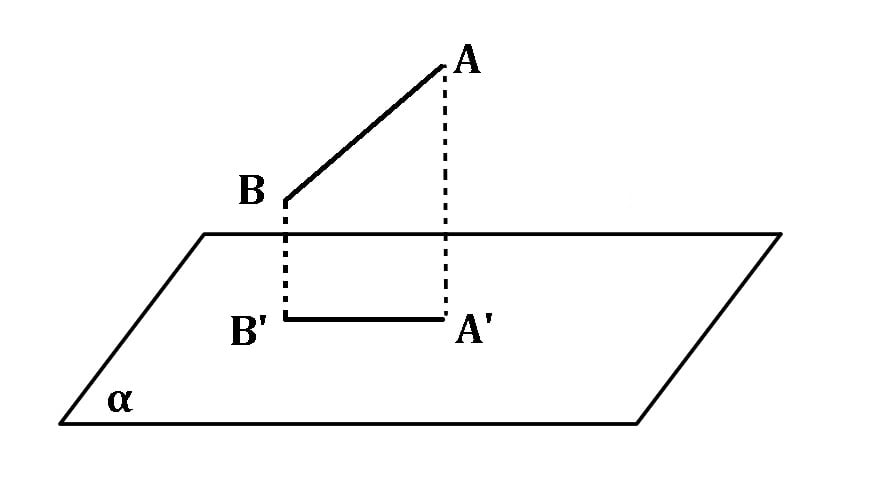
Proiecția segmentului AB pe planul α este un segment în acel plan, ale cărui capete reprezintă proiecțiile capetelor segmentului AB pe planul α.
prαA = A’, prαB = B’, A,B∉α => prαAB=A’B’
Unghiul dintre o dreaptă și un plan
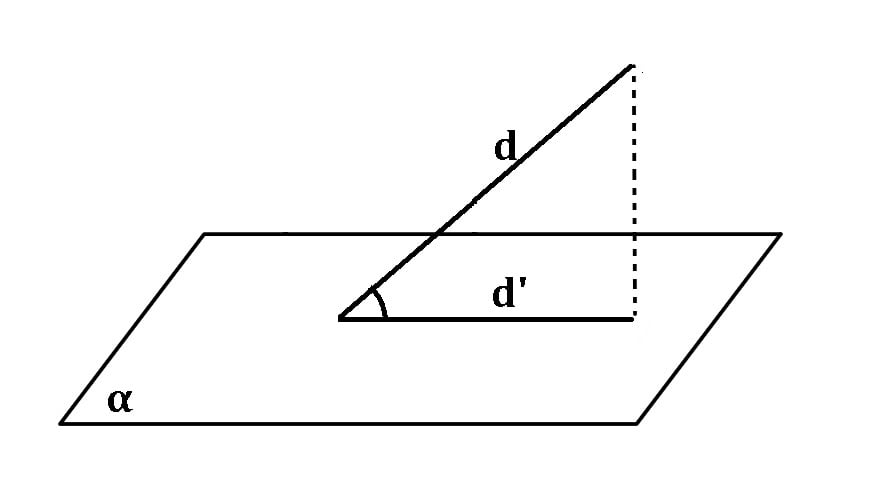
Unghiul dintre o dreaptă și un plan este unghiul format de acea dreaptă cu proiecția ei pe acel plan.
m∠(d,α) = m∠(d,d’) , unde d’ = prαd
Dacă o dreaptă este paralelă cu un plan, atunchi măsura unghiului dintre acea draptă și acel plan este de 0°.
Dacă o dreaptă este perpendiculară pe un plan, atunci măsura unghiului dintre acea dreaptă și acel plan este de 90°.
Unghiul diedru
Diedrul este firgura geometrică formată de două semiplane, mărginite de aceeași dreaptă.
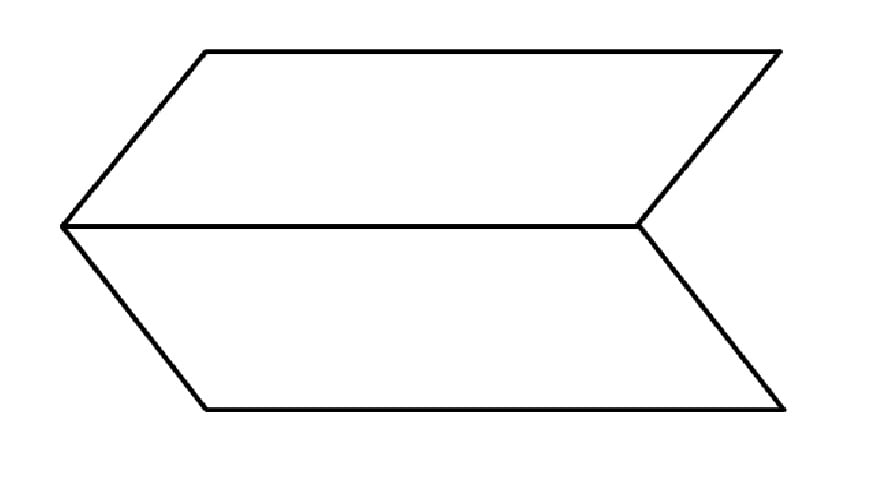
Unghiul plan al unghiului diedru este unghiul determinat de intersecția diedrului cu un plan perpendicular pe muchia sa.
Măsura unui unghi diedru este măsura unghiului plan corespunzător unghiului diedru.
Măsura unghiului dintre două plane este egală cu măsura unui diedru ascuțit sau drept format de acestea.
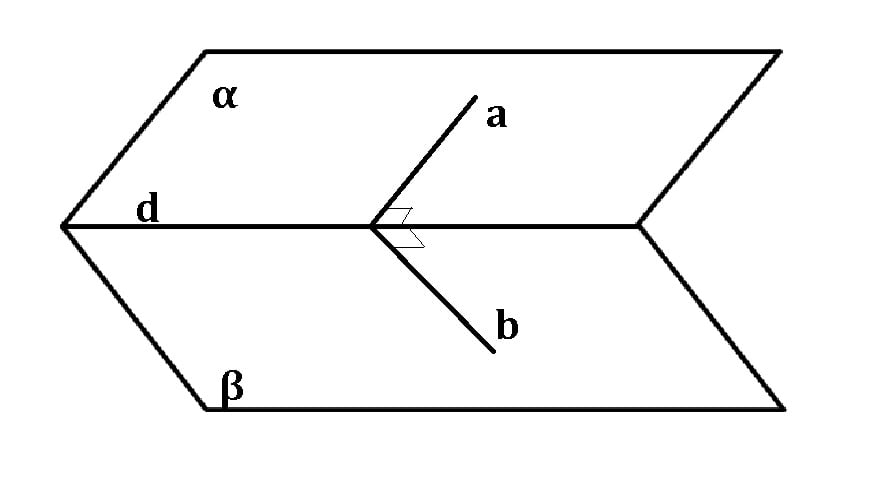
Măsura unghiului dintre două plane este egală cu măsura unghiului dintre o dreaptă din primul plan și o dreaptă din cel de-al doilea plan, ambele perpendiculare pe dreapta de intersecție a celor două plane.
m∠(α, β) = m∠(a, b), unde a∈α, b∈β, a⊥d, b⊥d, iar {d}=α∩β.
Dacă ți-a plăcut materialul despre Proiecții ortogonale în spațiu, nu uita să dai share paginii. Te aștept și la secțiunea Cursuri la matematică pentru a te înscrie la sesiunile de recapitulare.
