Calcul algebric în R. Material GRATUIT clasa a 8a.

Acest material despre calcul algebric în R cuprinde următoarele noțiuni: expresii algebrice, adunarea și scăderea numerelor reale reprezentate prin litere, înmulțirea, împărțirea și ridicarea la putere a numerelor reale reprezentate prin litere, formule de calcul prescurtat, metode de descompunere în factori, fracții algebrice, ecuația de gradul al doilea.

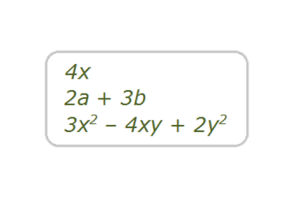
Expresii algebrice

O expresie algebrică este o succesiune de numere și/sau litere legate între ele prin operații aritmetice.

Exemplu:

E(x) = 2x² + 2x + 7

Adunarea și scăderea numerelor reprezentate prin litere

Termenii asemenea într-o expresie algebrică sunt termenii care conțin aceeași succesiune de litere, la aceiași exponenți.

Adunarea/ scăderea a doi termeni dintr-o expresie algebrică se face astfel: termenul asemenea rămâne același, iar coeficienții se adună/ scad.

Exemplu 1:

2x + 4x = (2+4)x = 6x

Observație: x este termenul asemenea, iar 2 și 4 sunt coeficienți.

Exemplu 2:

4xy + y² + 5x² – 7xy – 2y² – 5x² = (4-7)xy + (1-2)y² = -3xy – y²

Termenii opuși se reduc: +5x² cu -5x²

Am evidențiat cu aceeași culoare termenii care au aceeași parte literală. (4xy și 7xy cu galben și +y² și 2y² cu albastru)

Termenii cu aceeași parte literală se scad/adună între ei, copiind termenii asemenea li adunând/scăzând coeficienții.

Observație: Pentru ca y² nu are niciun coeficent în față, considerăm ca are coeficientul 1.

Înmulțirea, împărțirea și ridicarea la putere a numerelor reale reprezentate prin litere

Prin înmulțirea/ împărțirea a doi termeni dintr-o expresie algebrică se obține un nou termen astfel: se înmulțesc/împart între ei coeficienții și se înmulțesc/împart între ele numerele reprezentate prin litere.

Prin ridicarea a putere a unui termen dintr-o expresie algebrică se obține un nou termen, astfel: ridicăm la putere coeficientul și ridicăm la putere numerele reprezentate prin litere.

Exemplu:

2x²y · 4x³= (2·4) · (x²·x³) · y = 8 · x²⁺³· y = 8x⁵y

Formule de calcul prescurtat

Reamintim: (a+b)(c+d) = ac + bc + ad + bd

Exemplu:

(x+1)(x-4) = x² + x – 4x – 4 = x² – 3x – 4

Pătratul sumei a doi termeni:

(a+b)² = a² + 2ab + b²

Exemplu:

(2x + 7)² = (2x)² + 2 · 2x · 7 + 7² = 2² · x² + (2·2·7)·x + 49 = 4x² + 28x + 49

Pătratul diferenței a doi termeni:

(a-b)² = a² – 2ab + b²

Exemplu:

(a – 3b)² = a² – 2 · a · 3b + (3b)² = a² – (2·3) · a· b + 3² · b² = a² -6ab + 9b²

Produsul sumei și a diferenței a doi termeni

(a+b)(a-b) = a² – b²

Exemplu:

(1+5x)(1-5x) = 1² – (5x)² = 1 – 5² · x² = 1 – 25x²

Descompunerea în factori a unei expresii algebrice

Metoda factorului comun

Se folosește utilizând următoarele formule:

ab+ac = a(b+c)

ab-ac = a(b-c)

Exemplu:

4xy + 2xy² – 14x³y = 2xy (2 + y – 7x²)

Metoda restrângerii ca pătrat

Se folosește utilizând formulele:

a² + 2ab + b²=(a+b)²

a² – 2ab + b²=(a-b)²

Exemplu 1:

36x² +12xy + y² = 6² · x² + + y² = (6x)² + 2 · 6x · y + y² = (6x + y)²

Exemplu 2:

2y² – 10 $\sqrt{2}$ y + 25 = ( $\sqrt{2}$ ) ²y² – 2·5· $\sqrt{2}$ y + 5² = ( $\sqrt{2}$ y)² – 2 · $\sqrt{2}$ y · 5 + 5² = ( $\sqrt{2}$ y – 5)²

Metoda restrângerii ca diferență de pătrate

Se aplică utilizând formula:

a² – b² = (a-b)(a+b)

Exemplu:

49 – 16x²y⁴ = 7² – 4² · x² · (y²)² = 7² – (4xy²)² = (7-4xy²)(7+4xy²)

Metode combinate

Exemplu:

Descompuneți în factori: x² + 4x + 3

Varianta 1:

x² + 4x + 3 = x² + 4x + 4 – 1 = (x² + 4x + 4) – 1 = (x + 2)²– 1² = [(x+2)-1] · [(x+2)+1] = (x+1)(x+3)

Varianta 2:

Coeficientul lui x este +4, iar termenul liber este +3. Caut două numere care înmulțite dau +4, și înmulțite dau +3. Observ că acele numere sunt +1 și +3.

Rescriu expresia, astfel:

x² + 4x + 3 = x² + 1 · x + 3 · x + 1 · 3 = (x² + 1 · x) + (3 · x + 1 · 3) = x(x+1) + 3(x+1) = (x+1)(x+3).

Fracții algebrice

O fracție are sens dacă numitorul este diferit de 0.

Exemplu:

Fracția $\dfrac{2x+2}{x^2-1}$ are sens dacă x²-1 ≠ 0 ⟺ x² ≠ 1 ⟺ x ≠ 1 și x ≠ -1. Deci, fracția are sens pentru x ϵ R-{-1,1}.

Fracția $\dfrac{2x+2}{x^2-1}$ se simplifică astfel: $\dfrac{2x+2}{x^2-1}$ = $\dfrac{2(x+1)}{x^2-1^2}$ = $\dfrac{2(x+1)}{(x-1)(x+1)}$ . Simplificăm (x+1) de la numărător cu (x+1) de la numitor și obțin: $\dfrac{2}{x-1}$ .

Operații cu fracții algebrice

Exemplu:

Aduceți expresia la o formă cât mai simplă:

$\left(\dfrac{1}{x+1} - \dfrac{1}{x}\right)\cdot \dfrac{x^2-1}{2}$ =

aduc la același numitor, amplificând prima fracție cu x și a doua fracție cu (x+1)

= $\left[\dfrac{x}{x(x+1)} - \dfrac{(x+1)}{x(x+1)}\right]\cdot \dfrac {(x-1)(x+1)}{2}$

= $\left[\dfrac{x-x-1}{x(x+1)}\right] \cdot \dfrac{(x-1)(x+1)}{2}$

simplific pe diagonală (x+1) de la numitorul primei fracții cu (x+1) de la numărătorul celei de-a doua fracții

= $\dfrac{-1}{x} \cdot \dfrac{x-1}{2}$

= $\dfrac {-x+1}{2x}$

Ecuația de gradul al doilea

Rezolvarea ecuațiilor de forma ax² + bx + c = 0, a,b,c ϵ R, a≠0

a,b,c se numesc coeficienți;

x este necunoscuta.

Δ este discriminantul, unde Δ=b²-4ac

Avem trei situații:

Dacă Δ > 0, atunci avem fix două soluții reale: S = { $\dfrac{-b-\sqrt{\Delta}}{2a}$ ; $\dfrac{-b+\sqrt{\Delta}}{2a}$ }
Dacă Δ = 0, atunci avem fix o soluție reală: S = { $\dfrac{-b}{2a}$ }
Dacă Δ < 0, atunci nu avem soluții reale

Exemplu: x²-6x+5=0. Coeficienții sunt: a=1, b=-6, c=5. Δ = b²– 4ac = (-6)²-4·1·5 = 36-20 = 16 > 0

Deci avem două soluții reale: x₁= $\dfrac{6-\sqrt{16}}{2}$ = 1 și x₂ = $\dfrac{6+\sqrt{16}}{2}$ = 5.

S={1,5}

Utilizare Calcul algebric în R

Calculul Algebric în R este un instrument puternic care poate fi folosit în mai multe domenii, oferind soluții eficiente pentru rezolvarea problemelor matematice complexe.

În domeniul științific, Calculul Algebric în R poate fi utilizat pentru a analiza datele și a obține modele matematice care explică fenomenele naturale. De asemenea, poate fi folosit în domeniul financiar pentru a evalua investițiile și pentru a prezice tendințele pieței.

În inginerie, Calculul Algebric în R poate fi folosit pentru proiectarea și analizarea modelelor tehnice, precum și pentru simularea proceselor industriale și verificarea fiabilității acestora.

În domeniul social, Calculul Algebric în R poate fi utilizat pentru a analiza datele demografice și a prezice tendințele societății.

În concluzie, prin intermediul Calculului Algebric în R, se pot rezolva probleme complexe din mai multe domenii, oferind soluții eficiente și rapide.

Dacă ți-a plăcut materialul Calcul algebric în R, nu uita să dai share paginii. Te aștept și la secțiunea Cursuri la matem atică pentru a te înscrie la sesiunile de recapitulare.