
Geometrie în spațiu: pozițiile relative a două drepte în spațiu, relația de paralelism în spațiu, unghiuri cu laturile respectiv paralele, unghiul a două drepte în spațiu, drepte perpendiculare, pozițiile relative ale unei drepte față de un plan.
Pozițiile relative a două drepte în spațiu
Două drepte care au un singur punct comun se numesc drepte concurente.
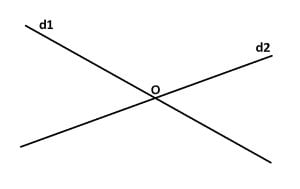
d1 ∩ d2 = {O}
Două drepte care se află în același plan și care nu au niciun punct comun se numesc drepte paralele.
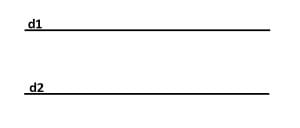
d1 || d2
Două drepte situate în același plan se numesc drepte coplanare.
Două drepte care nu sunt nici concurente și nici paralele sunt drepte necoplanare.
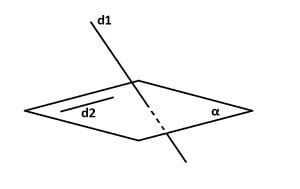
d1 ∩ d2 = Ø
d1 ∦ d2
Tranzitivitatea relației de paralelism în spațiu
Dacă două drepte distincte sunt paralele cu o a treia dreaptă , atunci dreptele sunt paralele între ele.

d1 || d3 și d2 || d3 => d1 || d2
Unghiul a două drepte în spațiu
Două unghiuri cu laturile respectiv paralele sunt:
- congruente (dacă amandouă sunt ascuțite sau amandouă sunt obtuze)
- suplementare (dacă unul dintre unghiuri este obtuz și celălalt ascuțit)
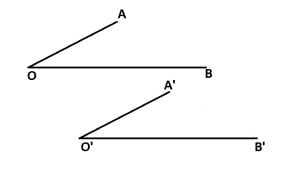
AO || A’O’
BO || B’O’
m![]() AOB = m
AOB = m![]() A’O’B’
A’O’B’
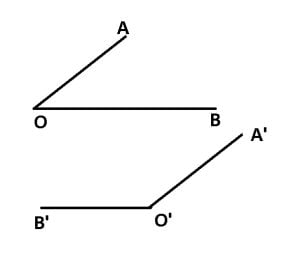
AO || A’O’
BO || B’O’
m![]() AOB + m
AOB + m![]() A’O’B’ = 180°
A’O’B’ = 180°
Unghiul a două drepte în spațiu reprezintă unghiul ascuțit sau drept cu vârful în orice punct al planului și cu laturile respectiv paralele cu dreptele date.
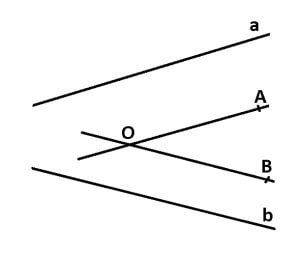
AO || a, BO || b și AO ∩ BO = {O} => m![]() (a;b) = m
(a;b) = m![]() (AO;OB) = m
(AO;OB) = m![]() AOB
AOB
Observație: unghiul dintre două drepte paralele are măsura de 0°.
Dacă măsura unghiului a două drepte în spațiu este de 90°, atunci ele se numesc drepte perpendiculare.
Pozițiile relative ale unei drepte față de un plan
- Dacă o dreaptă are două puncte comune cu un plan, atunci dreapta este conținută în acel plan.
- Dacă o dreaptă are un punct comun cu un plan, atunci dreapta intersectează planul.
- Dacă o dreaptă nu are niciun punct comun cu un plan, atunci dreapta este paralelă cu planul
- Teoremă: Dacă o dreaptă este paralelă cu o dreaptă din plan, atunci dreapta este paralelă cu planul.
Dreaptă conținută în plan:
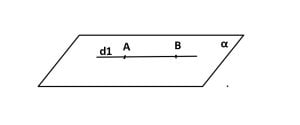
A și B ∈ α
A și B ∈ d
=> d ⊂ α
Dreaptă intersectată cu planul
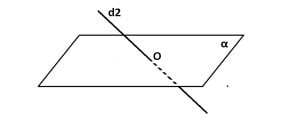
d2 ∩ α = {O}
Dreaptă paralelă cu planul
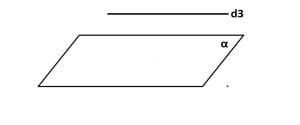
d3 ∩ α = Ø => d3 || α
O dreaptă este paralelă cu un plan dacă este paralelă cu o dreaptă conținută de acel plan.
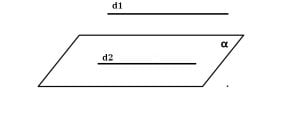
d1 || d2 și d2 ⊂ α => d1 || α
Dacă ți-a plăcut materialul de geometrie, nu uita să dai share paginii. Te aștept și la secțiunea Cursuri la matematică pentru a te înscrie la sesiunile de recapitulare.
