
Acest material despre divizibilitatea numerelor naturale cuprinde următoarele noțiuni: descompunerea în produs de puteri de numere prime, cel mai mare divizor comun, cel mai mic multiplu comun și proprietățile divizibilității pe N. Divizibilitatea numerelor naturale s-a studiat și în clasa a 5-a.
Descompunerea în produs de puteri de numere prime:
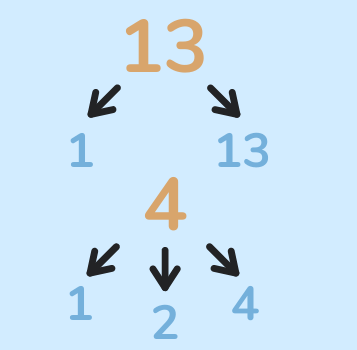
Un număr natural diferit de 1 care are ca divizori numai pe 1 și pe el însuși se numește număr prim.
Un număr prim are fix doi divizori: pe 1 și pe el însuși.
Numerele prime mai mici decât 50 sunt: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 și 47.
Observație: singurul număr prim și par este 2.
Un număr este compus dacă are cel puțin trei divizori (altfel spus, admite cel puțin un divizor propriu).
Un număr compus are trei sau mai mulți divizori.
Exemplu: Numărul 9 este compus, pentru că are trei divizori naturali: 1, 3 și 9.
Pentru a descompune un număr natural în produs de puteri de numere prime, împărțim, pe rând, numărul la numerele prime în ordine crescătoare, astfel:

Am împărțit de trei ori la 2, de două ori la 3 și o data la 5, deci 360 = 23 ![]() 32
32 ![]() 51
51
Determinarea celui mai mare divizor comun (c.m.m.d.c.) a două sau mai multe numere naturale
Pentru a afla c.m.m.d.c dintre două sau mai multe numere, parcurgem următorii pași:
- descompunem numerele în produs de puteri de factori primi
- alegem factorii comuni, o singură dată, la puterea cea mai mică, și îi înmulțim.
Exemplu: Aflați c.m.m.d.c dintre 360 și 108:
Descopunem:
360 = 23 ![]() 32
32 ![]() 51;
51;
108 = 22 ![]() 33
33
Factorii primi comuni ambelor numere sunt 2 și 3.
Cea mai mica putere a lui 2 este 22 și cea mai mică putere a lui 3 este 32.
22 ![]() 32 =36
32 =36
Deci (360,108) =36
Dacă cel mai mare divizor comun a două sau mai multe numere este 1, spunem că acele numere sunt prime între ele.
Determinarea celui mai mic multiplu comun a două sau mai multe numere naturale
Pentru a afla c.m.m.m.c dintre două sau mai multe numere naturale, parcurgem următorii pași:
- descompunem numerele în produs de puteri de factori primi
- alegem toți factorii, la puterea cea mai mare, o singură dată, și îi înmulțim.
Exemplu:
Aflați c.m.m.m.c dintre 360 și 108.
Descopunem:
360 = 23 ![]() 32
32 ![]() 51;
51;
108 = 22 ![]() 33
33
Factorii primi sunt 2, 3 și 5.
Cea mai mare putere a lui 2 este 23, cea mai mare putere a lui 3 este 33 și a cea mai mare putere a lui 5 este 51.
23 ![]() 33
33 ![]() 51 = 1080
51 = 1080
Deci [360,108] = 1080
Observație:
Pentru oricare două numere naturale a și b, avem:
(a, b) ![]() [a,b] = a
[a,b] = a![]() b
b
Proprietățile divizibilității în N
1|n, pentru orice n – număr natural. (adică orice număr natural este divizil cu 1)
n|n, pentru orice n – număr natural. (adică orice număr natural este divizil cu el însuși)
Pentru a,b,c, d numere naturale:
Dacă b|a și a|b, atunci a=b.
Dacă b|a și c|b, atunci c|a.
Dacă d|a și d|b, atunci d|a+b și d|a-b (a>b).
Material video
Dacă ți-a plăcut materialul despre Divizibilitatea numerelor naturale, nu uita să dai share paginii. Te aștept și la secțiunea Cursuri la matematică pentru a te înscrie la sesiunile de recapitulare.
