
Acest material despre mulțimi cuprinde următoarele noțiuni: reprezentarea mulțimilor, apartenența la o mulțime, mulțimi finite și infinite, cardinalul unei mulțimi, relații între mulțimi, operații cu mulțimi.
Mulțimile sunt formate din obiecte (numite elemente) care au o proprietate comună; ele sunt distincte și ordinea lor nu contează; o mulțime de numere se numește mulțime numerică.
Mulțimea vidă = mulțimea care nu are niciun element și se notează cu Ø.
Reprezentarea mulțimilor
- Prin enumerarea elementelor între acolade A={0,1,2,3,4}
- Prin proprietatea caracteristică A={n/ n natural, n<5}
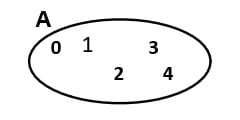
- Prin diagrama Venn-Euler:
Apartenența la o mulțime
Exemplu: Dacă A={0,1,2,3,4}, spunem că:
1 aparține mulțimii A și scriem 1ϵA;
6 nu se află în mulțimea A, deci 6 ∉ A
Mulțimi finite și infinite. Cardinalul unei mulțimi
Mulțime finită=mulțime cu un număr finit de elemente.
Exemplu: A={0,1,2,3,4} are 5 elemente, deci este finită.
Cardinalul unei mulțimi: card A sau |A| = numărul de elemente dintr-o mulțime finită.
Exemplu: A={0,1,2,3,4}
card A=5
Mulțime infinită=mulțime cu număr infinit de elemente.
Exemplu: N(mulțimea numerelor naturale)= {0,1,2,3,4,5 …}
Relații între mulțimi
Mulțimi egale: două mulțimi sunt egale dacă au aceleași elemente;
Exemplu: A={0,1,2,3,4}; B={0,1,2,3,4}, deci A=B
Submulțimea unei mulțimi: A este o submulțime a lui B dacă toate elementele din A sunt și în B.
Exemplu: A={0,1,2,3,4} și B={0,1,2,3,4,5,6}.
A este submulțime a lui B deoarece toate elementele din A, adică 0,1,2,3 și 4 se află și în mulțimea B.
Spunem că A⊂B (A inclus în B) sau B ⊃ A (B include pe A)
Fie mulțimea M={0,1,2,3}. Avem două tipuri de submulțimi:
- Submulțimi improprii (Ø și mulțimea însăși): submulțimile improprii ale lui M sunt si {0,1,2,3}.
- Submulțimi proprii (toate celelalte,dacă există):{0},{1},{2},{3},{0,1},{0,2},{0,3},{1,2},{1,3},{2,3},{0,1,2},{0,1,3},{0,2,3},{1,2,3}.
Operații cu mulțimi
Intersecția a două mulțimi A și B se notează A ∩ B și este formată din elementele comune mulțimilor A și B (care se află și în A și în B).
Exemplu: A={0,1,2,3,4}, B={3,4,5,6,7}.
A ∩ B={3,4}.
Reuniunea a două mulțimi A și B se notează A U B și este formată din toate elementele mulțimilor A și B (care se află în A sau în B)
Exemplu: A={0,1,2,3,4}, B={3,4,5,6,7}.
A U B={0,1,2,3,4,5,6,7}
Diferența a două mulțimi A și B se noteaza A-B sau A\B și este formată din elementele care se află în A și nu se află în B.
Exemplu: A={0,1,2,3,4}, B={3,4,5,6,7}.
A – B={0,1,2}
Dacă ți-a plăcut materialul, nu uita să dai share paginii. Te aștept și la secțiunea Cursuri la matematică pentru a te înscrie la sesiunile de recapitulare.
